
|
The Twelve Days of Christmas
Here's a familiar Christmas song: On the first day of Christmas, my true love sent to me A partridge in a pear tree On the second day of Christmas, my true love sent to me Two turtle doves, And a partridge in a pear tree ...and so forth, until the last verse: On the twelfth day of Christmas, my true love sent to me Twelve drummers drumming Eleven pipers piping Ten lords a-leaping Nine ladies dancing Eight maids a-milking Seven swans a-swimming Six geese a-laying Five gold rings Four calling birds Three French hens Two turtle doves And a partridge in a pear tree The Puzzle: How many gifts did my true love send me? To be clear, we'll interpret the song as stating that I received one gift (the partridge in a pear tree) on the first day, and three gifts on the second day (a partridge, and two turtle doves), and so on. If you are of a mathematical bent, figure out how many gifts I would receive on the Nth day, assuming the song could continue indefinitely. Hints will appear here! Try writing out the sum in rows and columns, where each row shows the number of gifts given on a particular day and each column represents a particular type of gift. For the general solution, you'll need to know the formula for the sum of the first N squares, or a little solid geometry. Here's the solution for the twelve days problem: 1 1 + 2 1 + 2 + 3 . . . 1 + 2 + 3 + ... + 12 ------------------------------------- 12x1 + 11x2 + 10x3 + ... + 1x12 = 364 From the diagram above, you can see that we get 12 partridges, 11x2 turtle doves, 10x3 french hens, and so on. Adding these up, we get 364 presents in total. One for each day of the year (except Christmas!)
That's a neat solution and it requires only 12 computations, but what if our true love was exceedingly generous and continued giving gifts. Let's say she keeps it up for 1000 days. Then how many gifts would we receive? Obviously, the above technique would be too laborious, so we need to find a better solution. I'll show you one algebraic and one geometric solution. The algebraic solution is much quicker, but requires the use of a formula that may not be known to all readers. Let's start with the geometric solution. A Geometric Approach to the Solution We can represent S(12) diagrammatically as follows: 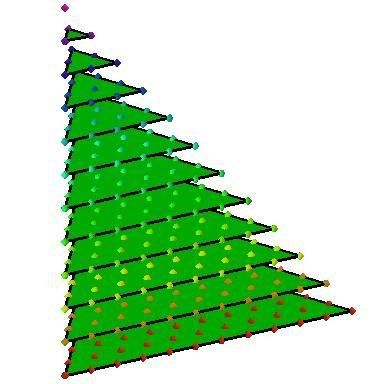
The kth layer of the "tree" has d(k) points. Essentially, we've created a triangular pyramid of presents. If you know some solid geometry, you'll have come across the formula for the volume of a pyramid: V= A h / 3, where A is the area of the base and h is the height. Though we're only counting grid points on the pyramid, it's reasonable to expect that we can approximate the number of presents by the volume of the corresponding pyramid. Let's do the problem in full generality and try to compute S(n). Now the height, h, is the number of days, n. The area of the base is n*n/2. So the volume of the pyramid is V(n) = n3/6. Unfortunately V(n) doesn't ever exactly equal S(n) (indeed, often V(n) isn't even a whole number!), so let's write S(n)=V(n)+E(n), where E(n) is an error term whose value we'd like to find. It's again reasonable to guess that E(n) is a polynomial, of degree smaller than V(n). So let's write: S(n)= n3/6 + a n2+ b n + c, for some constants a, b, and c. Plugging in the values of S(0), S(1), and S(2), we arrive at: 0 = S(0) = c from which we deduce a = 1/2, b= 1/3, and c=0. So assuming that E is indeed a quadratic polynomial, we deduce: S(n)=n3/6 + n2/2 + n/3. In particular, S(12)=123/6+122/2+12/3=364, and S(1000)=167,167,000. Note we haven't actually proved that this is the formula for S(n). Rather we've given plausible reasons for why this might be the formula. However, given our guess, one could use mathematical induction to prove the guess. I might go into this another day, but for the moment, we can contend ourselves with: An Algebraic Approach to the Solution d(k) = 1 + 2 + 3 + ... + k = k(k+1)/2presents, by the formula for the sum of the first k natural numbers. By the nth day, we'll have S(n) = d(1)+d(2)+...+d(k) = 1(1+1)/2 + 2(2+1)/2 + ... + n(n+1)/2presents. Expanding this out, we have: S(n) = (12 + 22 + ... + n2) /2 + (1 + 2 + 3 + ... + n)/2.Using the formula for the sum of the first n squares and the first n numbers, we have: S(n) = n(n+1)(2n+1)/12 + n(n+1)/4just as for the geometric solution. |
|